From The Vault: Diving into Big O, Big Theta, and Big Omega

Welcome to the first post in a new series I’m starting, “From The Vault”. In this series, I’ll be sharing some of the notes, thoughts, and insights I’ve recorded over the course of my studies in Software Engineering at Iowa State and beyond. These notes come from my personal vault (my Obsidian vault).

Today, we’re delving into the world of computational complexity, specifically focusing on Big O, Big Theta, and Big Omega. They are fundamental concepts in the study of algorithm efficiency and performance, and they were covered during my COM S 311 class at Iowa State University.

Note: While these notes are based on content directly from my vault, they have be parsed and re-organized prior to sharing to make more sense within a blog post.

Understanding Asymptotic Efficiency

Asymptotic Efficiency examines how the running time of an algorithm increases with the input size, particularly as the input size approaches infinity. It’s vital for evaluating algorithms beyond just raw execution times, which can vary between different hardware.

The Big Three of Computational Complexity

Big-O Notation ( $O$ )

Big-O gives an upper bound on the asymptotic behavior of a function, essentially defining the maximum rate at which the function can grow.

Mathematical Definition: If positive constants $c$ and $n_{0}$ exist such that $∀n \geq n_{0}, f(n) \leq c*g(n)$ , then $f ∈ O(g(n))$ .

It provides an asymptotic upper bound like $\leq$
When we discuss an algorithm having $O(n)$ complexity, it means the algorithm takes at most linear time relative to the input size

Size of $n$ based on input type:

Type	Input Size
integer	# of bits or digits
array	# of elements
string	length of string
graph	# of vertices or edges

Big-Omega Notation ( $\Omega$ )

Big-Omega is about the lower bound, indicating the minimum growth rate of a function.

Mathematical Definition: $\Omega(g(n)) = \{ f(n)\ |\ \text{There exist positive}\ c, n_{c}\ \text{such that}\ 0\leq cg(n) \leq f(n)\ ∀n \geq n_{0}\}$

It hints at the tightest lower bound of a function’s asymptotic behavior, like $\geq$

Big-Theta Notation ( $\Theta$ )

Big-Theta provides a tight bound, showing that a function grows precisely at a certain rate.

Definition: $\Theta(g(n)) = \{ f(n)\ |\ \text{There are positive}\ c_{1}, c_{2}, n_{0}\ \text{such that\ } ∀n \geq n_{0}, 0\leq c_{1}g(n) \leq f(n) \leq c_{2}g(n) \}$

It “sandwiches” the function $f(n)$ between $c_{1}g(n)$ and $c_{2}g(n)$ , denoting functions with the same growth rate

Simplifying with Examples

Big-O: If $f(n) =3n + 2$ , we simplify this to $O(n)$ , disregarding constants and lower order terms.

Big-Omega: For $f(n) = n^2 + 3n$ , we can say it’s $\Omega(n^2)$ , suggesting it grows at least as fast as $n^2$ .

Big-Theta: If we have $f(n) = 2n^2 + 3n + 1$ , it simplifies to $\Theta(n^2)$ , indicating it grows exactly as $n^2$ for large values of $n$ .

Examples from Class

Example 1

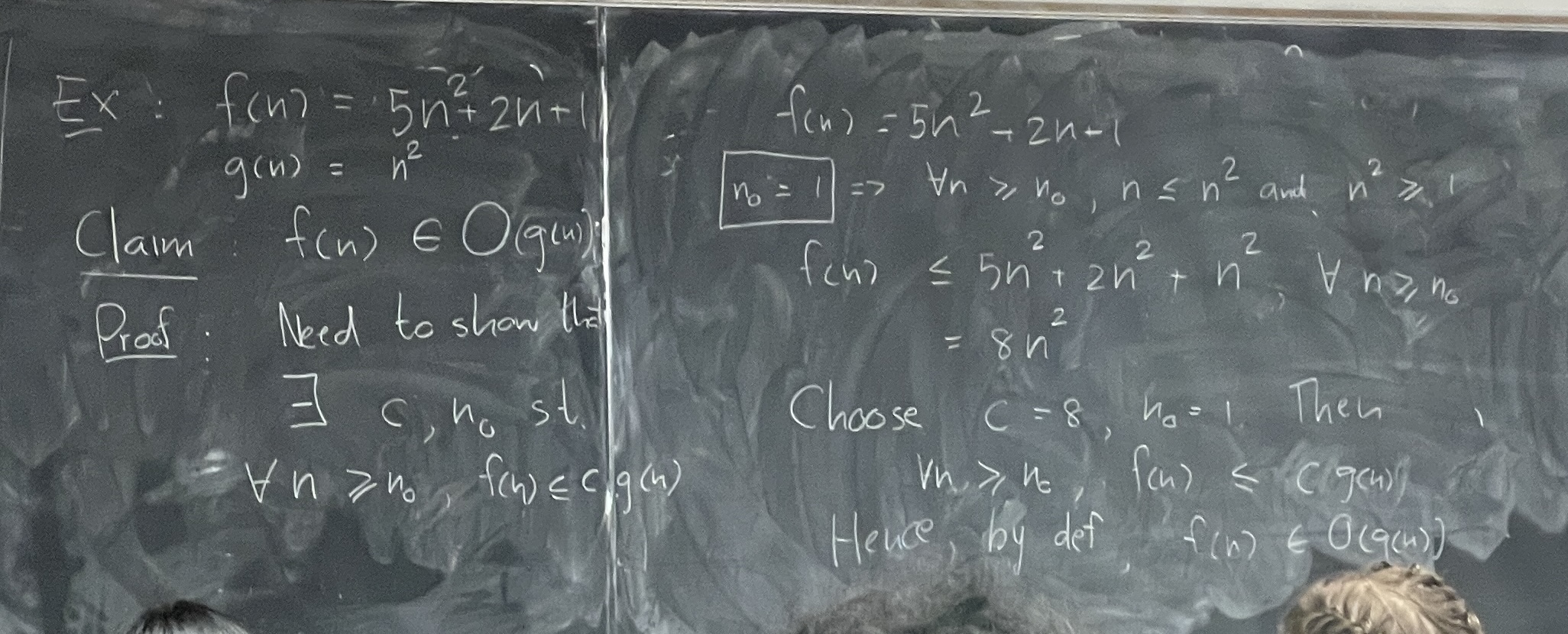
$f(n) =5n^{2}+2n+1$ and $g(n) = n^{2}$ Proof 1

Example 2

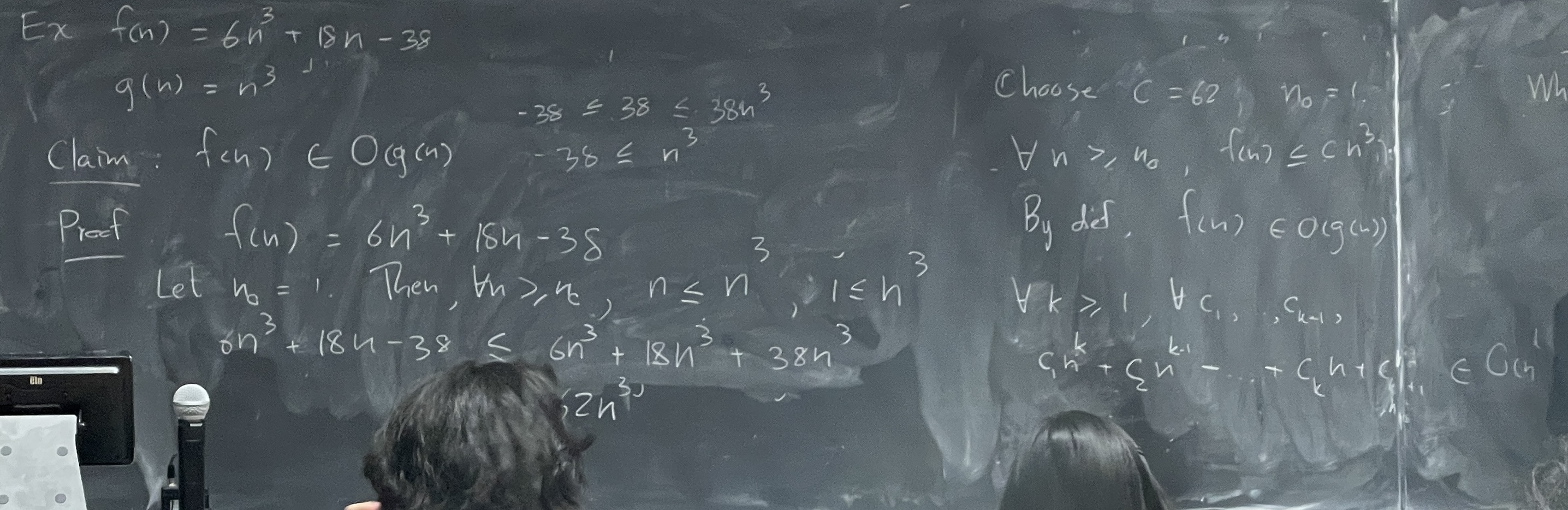
$f(n) = 6n^{3}+18n-38$ and $g(n) =n^3$ Claim: $f(n) ∈ O(g(n))$ Proof 1

Example 3

$n^{3} ∈ O(n^{2})$

Intuition tells us that $n^{3}$ grows faster than $n^{2}$

Claim: $n^{3} ∉ O(n^{2})$

Proof by contradiction:

Assume $n^{3} ∈ O(n^{2})$
By definition $∃ c, n_{0}$ such that $∀ n\geq n_{0}, n^3\leq cn^{2}$ → $n ∈ c$
But $c$ is a constant and an arbitrary $n$ cannot be smaller than $c$
This is a contradiction, so $n^{3} ∉ O(n^{2})$ must be true

Example 4

$f(n) = \log(n^{5})$ and $g(n)=\log(n)+5$

Claim: $f(n) ∈ O(g(n))$

Mathematical Rule: $\log(n^{k})=k\log(n)$

Proof:

$f(n)=\log(n^{5})=5\log(n)\leq 5\log(n)+25=5(\log(n)+5)=5g(n)$
Choose $c=5,n_{0}=1$ , $∀n\geq n_{0}, f(n) \leq cg(n)$
By definition, $f(n) ∈ O(g(n))$

Example 5

$f(n)=\log(n)$ and $g(n) =\sqrt{ n }$

Claim: $f(n) ∈ O(g(n))$

Proof:

Tangent: $\log_{10}(10^{9})=9\log_{10}(10)=9*1$
$f(n)=\log(n)=\log((n^{1/2})^2)=2\log(n^{1/2})=2\log(\sqrt{ n })$
$∀ n \geq 1, \log(n)\leq n\implies \log(\sqrt{n })\leq \sqrt{ n }$
$2\log(\sqrt{ n })\leq 2\sqrt{ n }=2g(n)$
Choose $c=2,n_{0}=1$ , $∀n \geq n_{0}, f(n) \leq cg(n)$
By definition, $f(n) ∈ O(g(n))$

Extra: Review of log

If $n=a^x$ , then $x=\log_{a}n$
$\log(a^{b})=b\log(a)$
$\log (a*b)=\log(a)+\log(b)$
$\log\left( \frac{a}{b} \right)=\log(a*b^{-1})=\log(a)+\log(b^{-1})=\log(a)-\log(b)$
$2^{\log_{2}(n)}=n$
$a^{\log_{b}(n)}=n^{\log_{b}(a)}$
$\log_{b}(x)=\frac{\log_{a}(x)}{\log_{a}(b)}$

Formal Derivations of Runtime

Expectation: Express runtime in Big-O notation

Example 1

for (i = 1; i <= n; i++) {
	print(i)
}

Goal: Derive runtime of this loop as a function of $n$ Analysis:

For each iteration: how many primitive operations are done?
There’s a comparison (i <= n), print, and increment → all of these are constant runtime
Let $c$ be the number of primitive operations being done in one iteration
During each iteration, $c$ primitive operations are done

i	# Primitive Operations
1	c
2	c
3	c
…	…

This sums to $c+c+\dots +c$ or $n$ times
Therefore, the total number of primitive operations is $\sum_{i=1}^{n}c=c*n=O(n)$
Thus, the runtime of this algorithm is $O(n)$

Example 2

for (i = 1; i <= n; i++) {
	for (j = 1; j <= n; j++) {
		// constant # of primitive operations
	}
}

Analysis:

Start with innermost loop → Each iteration consists of a constant number of primitive operations, say $c_{1}$ operations, from previous example we know that the number of primitive operations is $\sum_{j=1}^nc_{1}=O(n)$
For a single iteration of the outer loop, the number of primitive operations is the inner loop sum + comparison operations + increment etc.
Call the comparison and increment operations for the outer loop $c_{2}$
Total runtime is $\sum_{i=1}^n\left((( \sum_{j=1}^nc_{1})+c_{2} \right)$ → $\sum_{i+1}^{n}(c_{1 }n+c_{2})=\sum_{i=1}^{n}c_{1}n +\sum_{i=1}^nc_{2}=c_{1}n^{2}+c_{2}n$
With a polynomial runtime, we clear lower order terms and remove constants, therefore the runtime is $O(n^{2})$

Example 3

for (i = 1; i <= n; i++) {
	for (j=1; j <= i; j++) {
		// constant # of primitive operations
	}
}

Analysis:

Start with the innermost loop → Each iteration consists of a constant number of primitive operations, say $c_{1}$ operations
However, in this case, the inner loop doesn’t run $n$ times every iteration of the outer loop
Instead, it runs $i$ times. Therefore, for each iteration $i$ of the outer loop, the number of primitive operations the inner loop does is $\sum_{j=1}^{i}c_{1}$
Now, we can sum this over all $n$ iterations of the outer loop to get the total number of primitive operations: $\sum_{i=1}^{n}(\sum_{j=1}^{i}c_{1} + c_{2})$ , where $c_2$ is the constant runtime from the comparison and increment operations of the outer loop
From this, we can rewrite the sum as: $c_{1}(\sum_{i=1}^{n}i)+nc_{2}$ → since $\sum_{i=1}^{n}i=\frac{1}{2}n(n+1)$
Simplifying, we find this to be $c_{1} \frac{n(n+1)}{2} + c_{2}n$
In big-O notation, we ignore lower order terms and constants, therefore the runtime is $O(n^{2})$

This highlights an important point: a loop running $n$ times nested within another loop running $n$ times does not always result in a runtime of $O(n^2)$ . In this case the inner loop only runs $i$ times for the $i$ th iteration of the outer loop. The analysis still results in $O(n^2)$ , but the actual number of operations is less than the previous example where both loops ran $n$ times.

I must admit, these notes, although relatively comprehensive, have room for improvement. So far, I’ve found the study of Big O, Big Theta, and Big Omega challenging when understood via proofs.

My plan is to revisit and add to these notes as my understanding of the subject continues to grow. This is a journey, and I believe in the power of constant learning and improvement. Sharing these notes publicly isn’t just about providing a resource to others; it’s also about motivating myself.

By putting my notes out there, I’m compelled to take better, more deliberate notes during class. It’s a commitment to myself to strive for clarity in understanding and precision in note-taking. I hope that my journey will inspire you in some way and lead to shared growth.